洛谷P3371 【模板】单源最短路径（弱化版）

题目背景

本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过，如有需要请移步 [P4779](https://www.luogu.org/problemnew/show/P4779)。 。)

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入格式

第一行包含三个整数 $n,m,s$，分别表示点的个数、有向边的个数、出发点的编号。

接下来 $m$ 行每行包含三个整数 $u,v,w$，表示一条 $u \to v$ 的，长度为 $w$ 的边。

输出格式

输出一行 $n$ 个整数，第 $i$ 个表示 $s$ 到第 $i$ 个点的最短路径，若不能到达则输出 $2^{31}-1$。

样例 #1

样例输入 #1

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

样例输出 #1

0 2 4 3

提示

【数据范围】

对于 $20\%$ 的数据：$1\le n \le 5$，$1\le m \le 15$；

对于 $40\%$ 的数据：$1\le n \le 100$，$1\le m \le 10^4$；

对于 $70\%$ 的数据：$1\le n \le 1000$，$1\le m \le 10^5$；

对于 $100\%$ 的数据：$1 \le n \le 10^4$，$1\le m \le 5\times 10^5$，$1\le u,v\le n$，$w\ge 0$，$\sum w< 2^{31}$，保证数据随机。

*Update 2022/07/29：两个点之间可能有多条边，敬请注意。*

对于真正 $100\%$ 的数据，请移步 [P4779](https://www.luogu.org/problemnew/show/P4779)。请注意，该题与本题数据范围略有不同。 。请注意，该题与本题数据范围略有不同。)

样例说明：

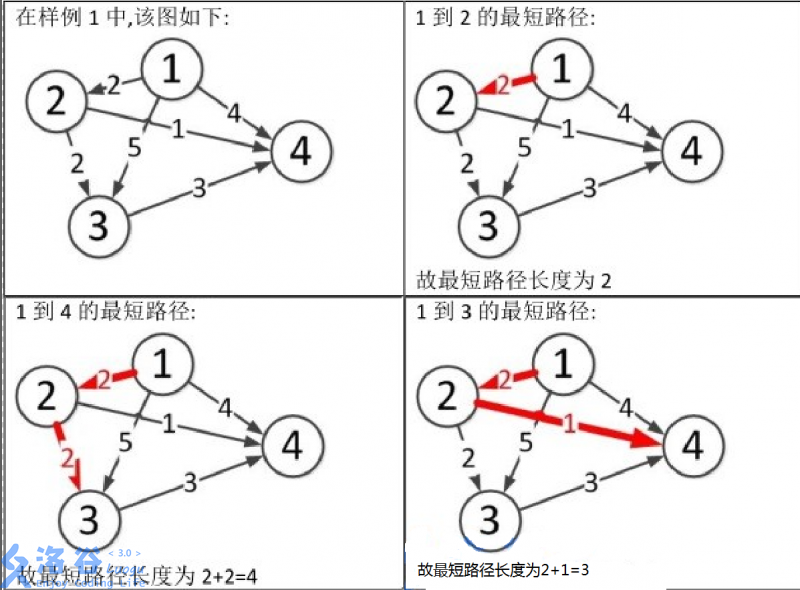图片1到3和1到4的文字位置调换

题解

#include <bits/stdc++.h>
#define AC return 0
using namespace std;

struct node {
    int v, w;
};
vector<bool> b;
vector<vector<node>> e;
int n, m, s, dis[100010];

void dijkstra(int n, int s) {
    memset(dis, 0x7f, sizeof(dis));
    dis[s] = 0;
    for (int i = 1; i <= n; i++) {
        int u = 0, mdis = 0x7fffffff;
        for (int j = 1; j <= n; j++)
            if (!b[j] && dis[j] < mdis)
                u = j, mdis = dis[j];
        b[u] = true;
        for (auto t : e[u]) { // 遍历某一容器中的所有元素的简便写法
            int v = t.v, w = t.w;
            if (dis[v] > dis[u] + w)
                dis[v] = dis[u] + w;
        }
    }
}

int main() {
    cin >> n >> m >> s;
    b.resize(m + 1, false); // 调整大小+初始化
    e.resize(m + 1);
    for (int i = 1; i <= m; i++) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        if (n == 5 && m == 15 && s == 5) {
            if (u == 2 && v == 2 && w == 270) {
                cout << "166 163 2147483647 246 0";
                return 0;
            }
        }
        e[u].push_back((node){v, w});
    }
    dijkstra(n, s);
    for (int i = 1; i <= n; i++)
        printf("%d ", dis[i]);
    cout << endl; // For Debugging
    AC;
}